If you are developing a deep learning model, overfitting is the most prevalent word that comes to mind, whether you are a beginner or an expert in the area. Overfitting revolves around the perfectly fitting training data on the model and when this happens the algorithm fails to achieve its objective. This is where we need regularization techniques to deal with the overfitting problems.
This blog discusses the problem of overfitting and how regularization aids in the accomplishment of the goal of deep learning models.
The blog's structure is intended to focus on the following topics:
- What is overfitting?
- What is Regularization?
- Why Regularization?
- How does Regularization work?
- Techniques of Regularization
- L1 Regularization
- L2 Regularization
- The Key differences between L1 and L2 Regularization
- Dropout regularization
- Takeaways
What is Overfitting?
Simply put, when a model trains on sample data for an excessively long time or becomes very complicated, it may begin to learn "noise," or unimportant information, from the dataset. The model becomes "overfitted" and unable to generalize successfully to new data when it memorizes the noise and fits the training set too closely. A model won't be able to carry out the classification or prediction tasks that it was designed for if it can't generalize successfully to new data.
What is Regularization?
When completely new data from the problem domain is fed as an input into deep learning models, regularization is a collection of strategies that can assist prevent overfitting in neural networks and improve their accuracy by modifying the learning procedure slightly such that the model generalizes more successfully. The model then performs better on the unobserved data as a result.
Why Regularization?
Through Regularization the bigger coefficient input parameters receive a "penalty", which ultimately reduces the variance of the model, and particularly in deep learning the nodes' weight matrices are penalized. With regularization, a more optimized and better accurate model for better output is achieved.
How does Regularization work?
When modeling the data, a low bias and high variance scenario is referred to as overfitting. To handle this, regularization techniques trade more bias for less variance. Effective regularization is one that strikes the optimal balance between bias and variation, with the final result being a notable decrease in variance at the least possible cost to bias. This would imply low variation without significantly raising the bias value, to put it another way.
Additionally, Regularization orders possible models from weakest overfit to biggest and adds penalties to more complicated models. Regularization makes the assumption that the least weights could result in simpler models and help prevent overfitting.
Techniques of Regularization
So as we now have a better understanding of what overfitting is and how regularization helps in making deep learning models better and more effective, now let's shift our focus to the techniques that we need to use for regularization in deep learning.
L1 Regularization
Essentially, the L1 regularizer searches for parameter vectors that minimize the parameter vector's norm (the length of the vector). The main issue here is how to best optimize the parameters of a single neuron, a single layer neural network generally, and a single layer feed-forward neural network specifically.
Since L1 regularization offers sparse solutions, it is the favored method when there are many features. Even so, we benefit from the computational advantage since it is possible to omit features with zero coefficients.
The mathematical representation for the L1 regularization is:
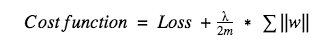
Here the lambda is the regularization parameter. Here we penalize the absolute value of the weights and weights may be reduced to zero. Hence L1 regularization techniques come very handily when we are trying to compress the deep learning model.
L2 Regularization
By limiting the coefficient and maintaining all the variables, L2 regularization helps solve problems with multicollinearity (highly correlated independent variables). The importance of predictors may be estimated using L2 regression, and based on that, the unimportant predictors can be penalized.
The mathematical representation for the L2 regularization is:

The regularization parameter, in this case, is lambda. The value of this hyperparameter is generally tweaked for better outcomes. Since L2 regularization leads the weights to decay towards zero(but not exactly zero ), it is also known as weight decay.
The key differences between L1 and L2 Regularization
A regression model is referred to as Lasso Regression if the L1 Regularization method is used and Ridge Regression is the term used if the L2 regularization method is employed.
The penalty for L1 regularization is equal to the amount of the coefficient in absolute terms. With this form of regularization, sparse models with few coefficients may be produced. It's possible that certain coefficients will go to zero and be dropped from the model. Coefficient values are closer to zero when the penalties are higher (ideal for producing simpler models).
On the other hand, sparse models or coefficients are not eliminated by L2 regularization. As a result, as compared to the Ridge, Lasso Regression is simpler to understand.
Apart from this, there are a few other factors where the L1 regularization technique differs from the L1 regularization. These factors are as follows:
- L1 regularization can add the penalty term to the cost function by taking the absolute value of the weight parameters into account. On the other hand, the squared value of the weights in the cost function is added via L2 regularization.
- In order to avoid overfitting, L2 regularization makes estimates for the data mean instead of the median as is done by L1 regularization.
- Since L2 is a square of weight, it has a closed-form solution; however, L1, which is a non-differentiable function and includes an absolute value, does not. Due to this, L1 regularization requires more approximations, is computationally more costly, and cannot be done within the framework of matrix measurement.
Dropout Regularization
Dropout is a regularization method in which certain neurons are disregarded at random. They "drop out" at random. This means that any weight changes are not applied to the neuron on the backward trip and that their effect on the activation of downstream neurons is temporally erased on the forward pass. Neuron weights inside a neural network find their place in the network as it learns.
Neuronal weights are customized for particular characteristics, resulting in some specialization. Neighboring neurons start to depend on this specialization, which, if it goes too far, might produce a fragile model that is overly dependent on the training data, which can be dangerous.
In the dropout regularization technique, complex co-adaptations are used to describe how a neuron becomes dependent on circumstances during training.
Takeaways
Regularization plays a crucial role in Deep Neural Network training. All of the aforementioned tactics may be divided into two broad groups. At some point throughout the training lifespan, they either penalize the trainable parameters or the introduced noise. Whether this is on the target labels, the trainable parameters, the network design, or the training data.
L1 regularization is used to reduce the number of features in a massive, dimensional dataset by producing output for the model's features as binary weights ranging from 0 to 1.
L2 regularization disperses the error terms among all weights, resulting in more precise final models that are specifically tailored.
And, dropout is a regularization technique that produces a "thinned" network with distinct combinations of the hidden layer units being deleted at random intervals throughout the training process.
Just to mention, you can not have a high accuracy working model without the use of regularization techniques. And apart from L1, L2, and Dropout regularization techniques, there are a few other regularization techniques that are out of the scope of this article, we might try to cover them for you in a different article.
As of now, our quest toward regularization comes to an end. If you have any inquiries, please do not hesitate to contact us. As always, feel free to share it if you find it useful.